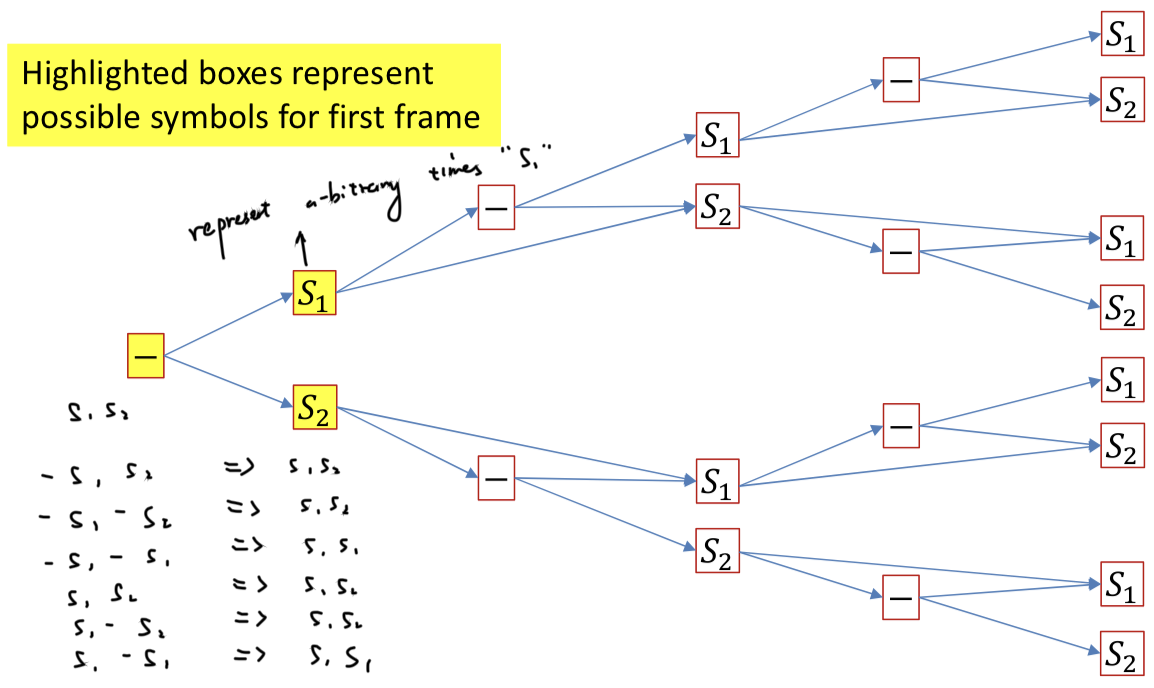
Sequence to sequence
- Sequence goes in, sequence comes out
- No notion of “time synchrony” between input and output
- May even nots maintain order of symbols (from one language to another)
With order synchrony
- The input and output sequences happen in the same order
- Although they may be time asynchronous
- E.g. Speech recognition
- The input speech corresponds to the phoneme sequence output
- Question
- How do we know when to output symbols
- In fact, the network produces outputs at every time
- Which of these are the real outputs?
Option 1
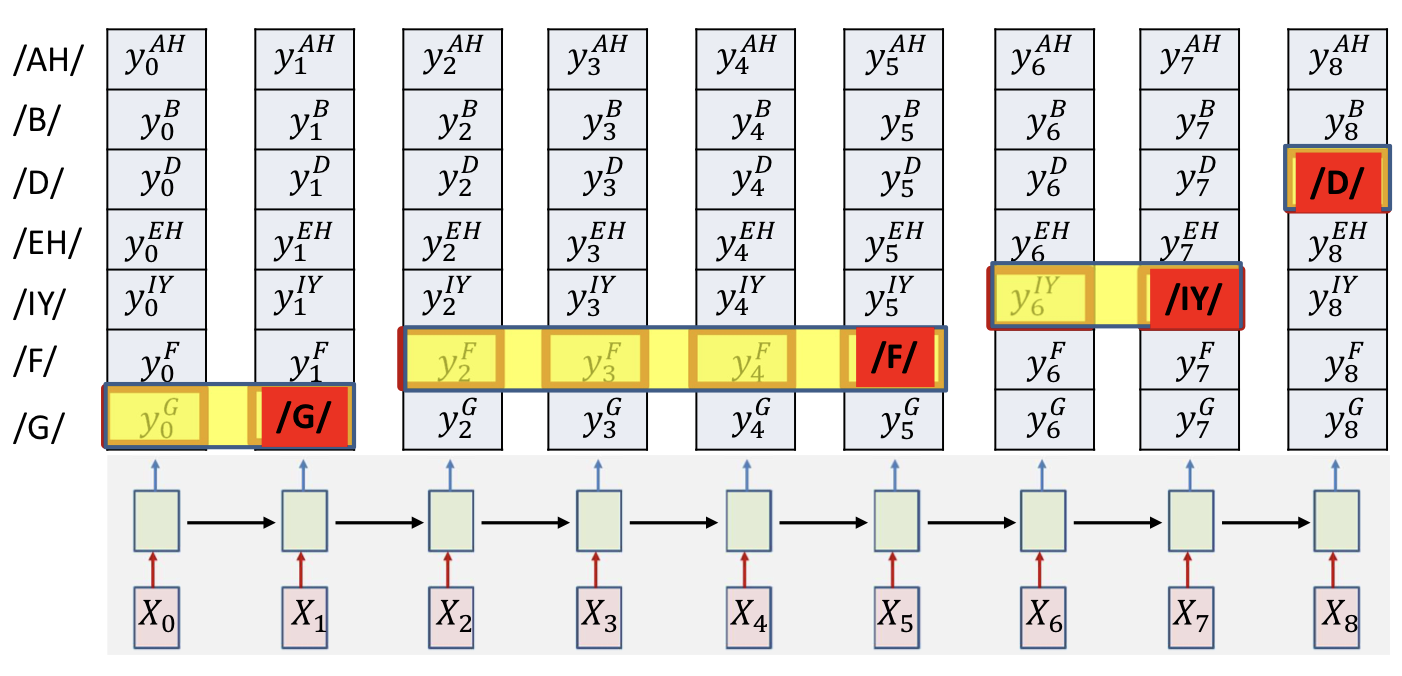
- Simply select the most probable symbol at each time
- Merge adjacent repeated symbols, and place the actual emission of the symbol in the final instant
- Problem
- Cannot distinguish between an extended symbol and repetitions of the symbol
- Resulting sequence may be meaningless
Option 2
- Impose external constraints on what sequences are allowed
- E.g. only allow sequences corresponding to dictionary words
Decoding
The process of obtaining an output from the network
Time-synchronous & order-synchronous sequence
aaabbbbbbccc => abc (probility 0.5) aabbbbbbbccc => abc (probility 0.001) cccddddddeee => cde (probility 0.4) cccddddeeeee => cde (probility 0.4)- So abc is the most likely time-synchronous output sequence
- But cde is the the most likely order-synchronous sequence
Option 2 is in fact a suboptimal decode that actually finds the most likely time-synchronous output sequence
The “merging” heuristics do not guarantee optimal order-synchronous sequences
No timing information provided
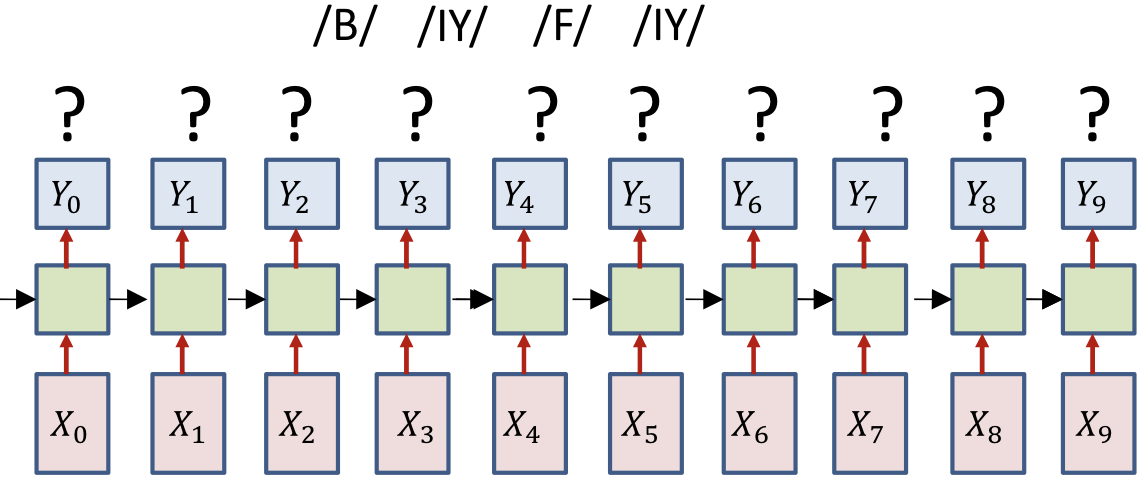
- Only the sequence of output symbols is provided for the training data
- But no indication of which one occurs where
Guess the alignment
- Initialize
- Assign an initial alignment
- Either randomly, based on some heuristic, or any other rationale
- Iterate
- Train the network using the current alignment
- Reestimate the alignment for each training instance
Constraining the alignment
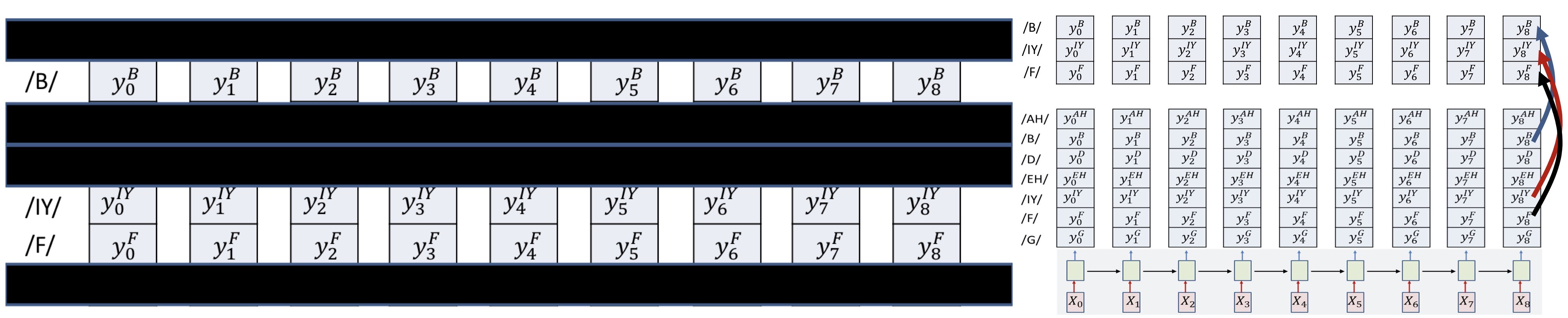
- Try 1
- Block out all rows that do not include symbols from the target sequence
- E.g. Block out rows that are not /B/ /IY/ or /F/
- Only decode on reduced grid
- We are now assured that only the appropriate symbols will be hypothesized
- But this still doesn’t assure that the decode sequence correctly expands the target symbol sequence
- Order variance
- Try 2
- Explicitly arrange the constructed table
- Arrange the constructed table so that from top to bottom it has the exact sequence of symbols required
- If a symbol occurs multiple times, we repeat the row in the appropriate location

Constrain that the first symbol in the decode must be the top left block
- The last symbol must be the bottom right
- The rest of the symbols must follow a sequence that monotonically travels down from top left to bottom right
- This guarantees that the sequence is an expansion of the target sequence
Compose a graph such that every path in the graph from source to sink represents a valid alignment
- The “score” of a path is the product of the probabilities of all nodes along the path
- Find the most probable path from source to sink using any dynamic programming algorithm (viterbi algorithm)
Viterbi algorithm
- Main idea
- The best path to any node must be an extension of the best path to one of its parent nodes
Dynamically track the best path (and the score of the best path) from the source node to every node in the graph
- At each node, keep track of
- The best incoming parent edge (BP)
- The score of the best path from the source to the node through this best parent edge (Bscr)
- At each node, keep track of
Process
- Algorithm
Gradients
- The gradient w.r.t the -th output vector
Problem
- Approach heavily dependent on initial alignment
- Prone to poor local optima
- Because we commit to the single “best” estimated alignment
- This can be way off, particularly in early iterations, or if the model is poorly initialized
Alternate view
- There is a probability distribution over alignments of the target Symbol sequence (to the input)
- Selecting a single alignment is the same as drawing a single sample from it
Instead of only selecting the most likely alignment, use the statistical expectation over all possible alignments
Use the entire distribution of alignments
This will mitigate the issue of suboptimal selection of alignment
Using the linearity of expectation
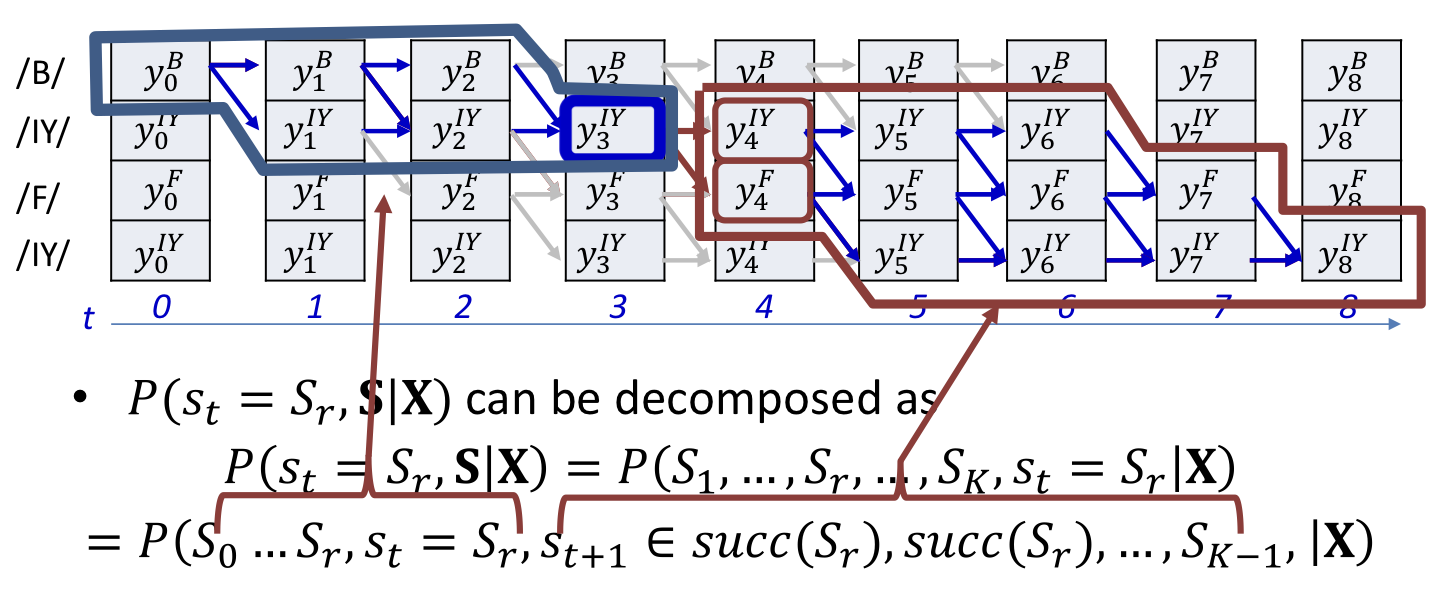
A posteriori probabilities of symbols
is the probability of seeing the specific symbol at time , given that the symbol sequence is an expansion of and given the input sequence
- is the total probability of all valid paths in the graph for target sequence that go through the symbol (the symbol in the sequence ) at time
- For a recurrent network without feedback from the output we can make the conditional independence assumption
- We will call the first term the forward probability
- We will call the second term the backward probability
Forward algorithm
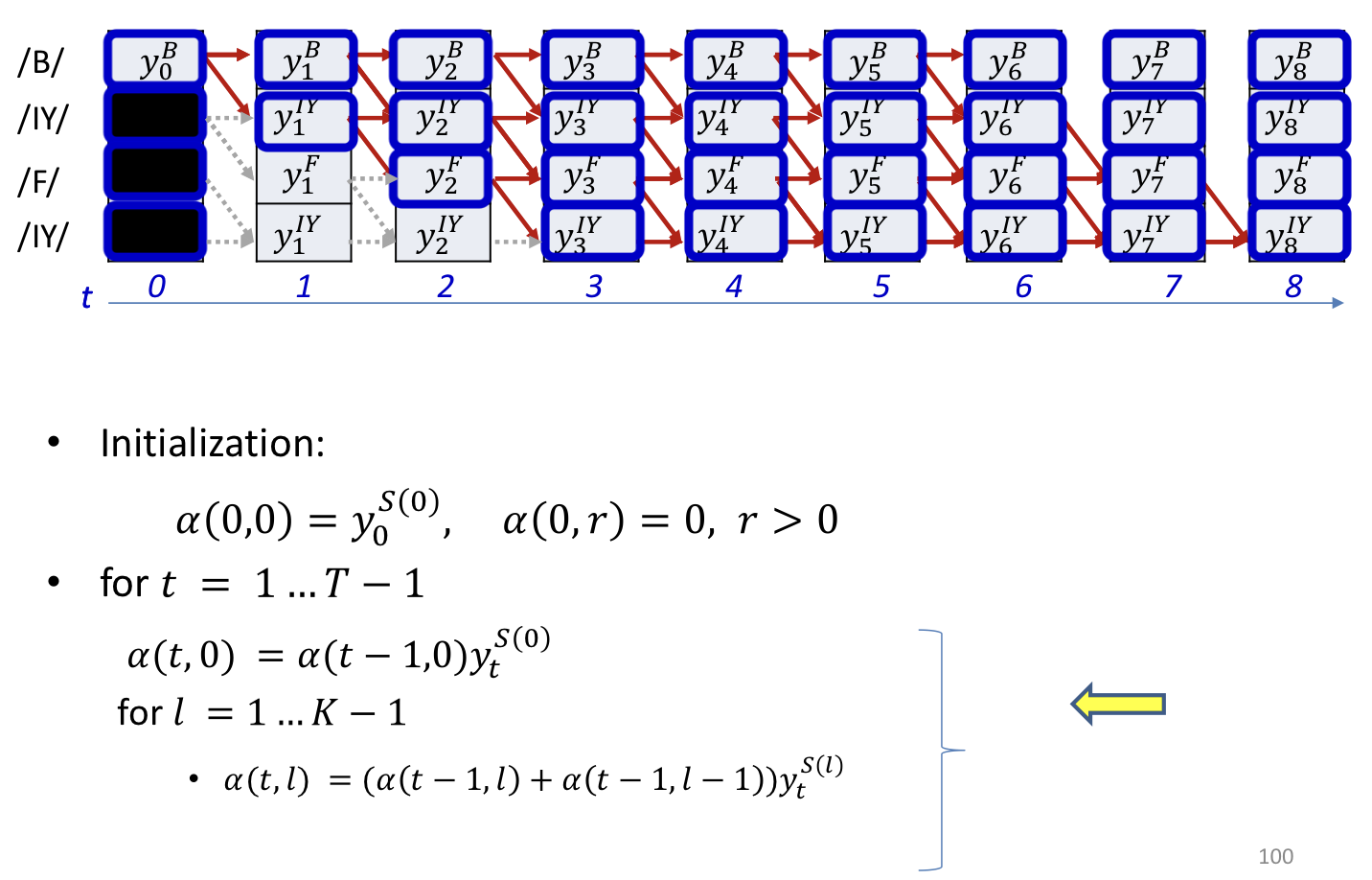
- In practice the recursion will gererally underflow
- Instead we can do it in the log domain
Backward algorithm

The joint probability
- Need to be normalized, get posterior probability
- We can also write this using the modified beta formula as (you will see this in papers)
The expected divergence
- The derivative of the divergence w.r.t the output of the net at any time
Compare to Viterbi algorithm, components will be non-zero only for symbols that occur in the training instance
Compute derivative
- Normally we ignore the second term, and think of as a maximum-likelihood estimate
- And the derivatives at both these locations must be summed if occurs repetition
Repetitive decoding problem
- Cannot distinguish between an extended symbol and repetitions of the symbol
- We have a decode: R R R O O O O O D
- Is this the symbol sequence ROD or ROOD?
- Solution: Introduce an explicit extra symbol which serves to separate discrete versions of a symbol
- A “blank” (represented by “-”)
- RRR---OO---DDD = ROD
- RR-R---OO---D-DD = RRODD
Modified forward algorithm
- A blank is mandatory between repetitions of a symbol but not required between distinct symbols
- Skips are permitted across a blank, but only if the symbols on either side are different
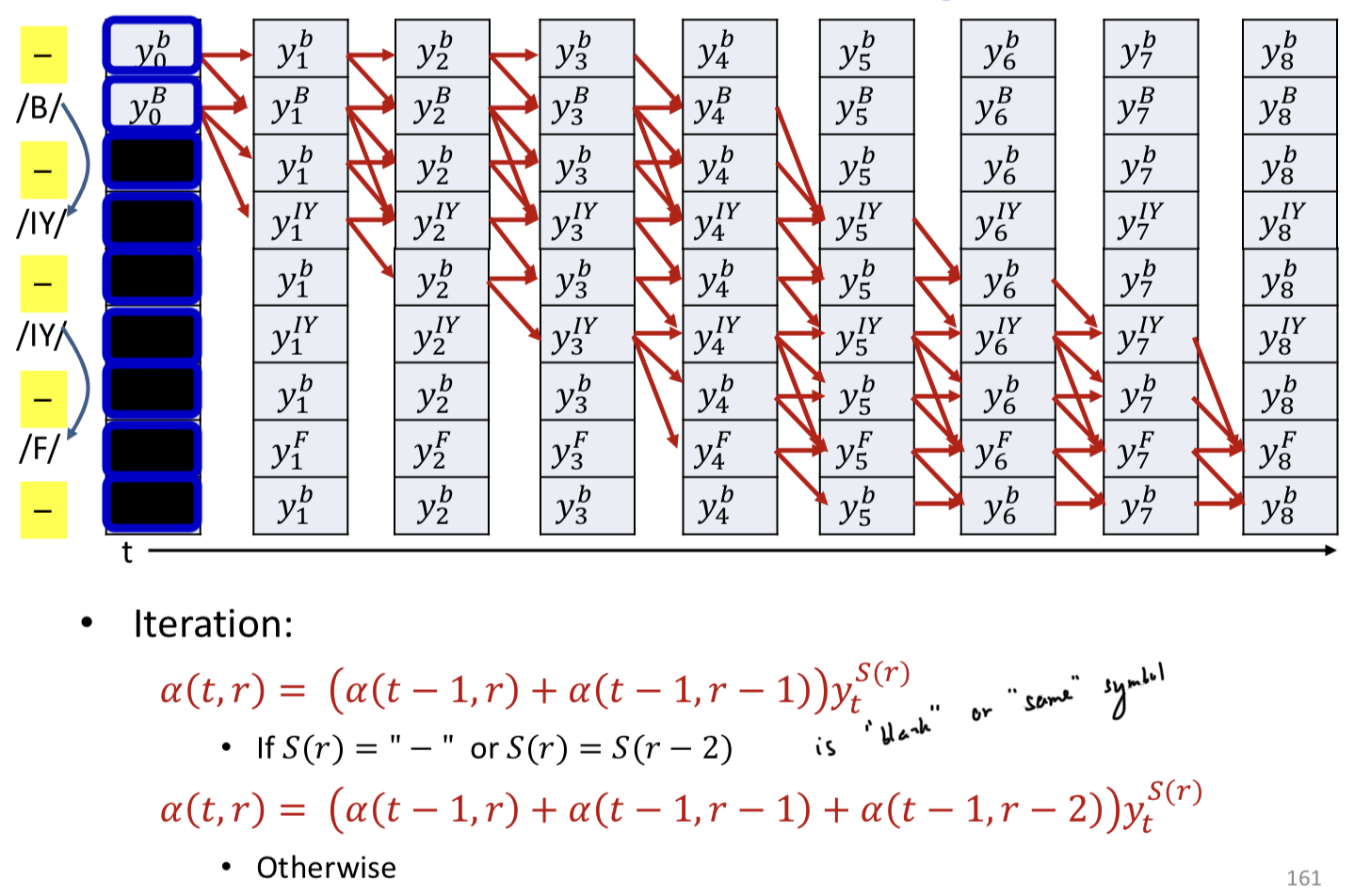
Modified backward algorithm
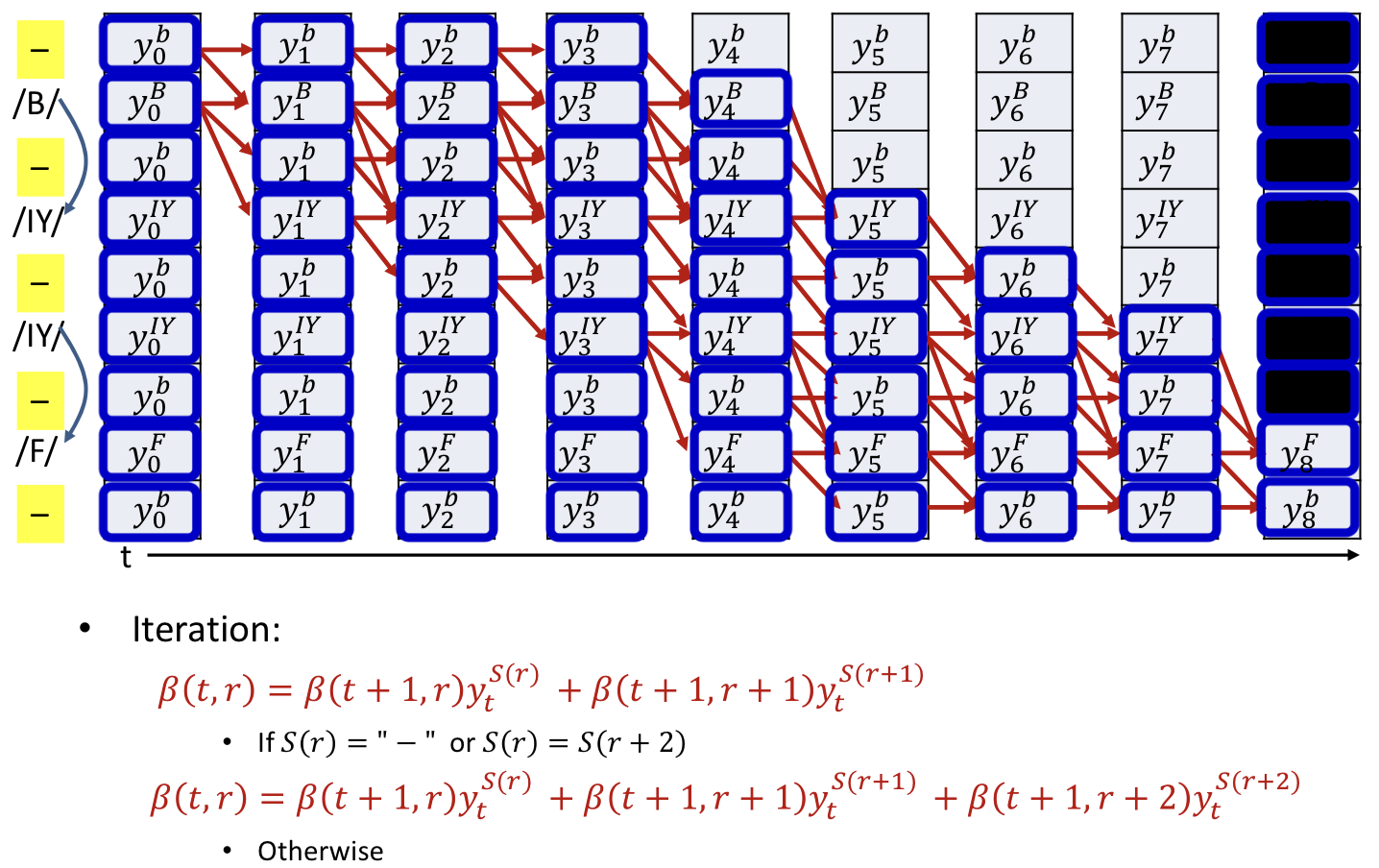
Overall training procedure
Setup the network
- Typically many-layered LSTM
Initialize all parameters of the network
- Include a 「blank」 symbol in vocabulary
Foreach training instance
- Pass the training instance through the network and obtain all symbol probabilities at each time
- Construct the graph representing the specific symbol sequence in the instance
Backword pass
Perform the forward backward algorithm to compute and
Compute derivative of divergence for each
- Aggregate derivatives over minibatch and update parameters
CTC: Connectionist Temporal Classification
- The overall framework is referred to as CTC
- This is in fact a suboptimal decode that actually finds the most likely time-synchronous output sequence
- Actual decoding objective
- Explicit computation of this will require evaluate of an exponential number of symbol sequences
Beam search
- Only used in test
- Uses breadth-first search to build its search tree
- Choose top k words for next prediction (prone)